4.ÜNİTE:ÜÇGENLER

ÜÇGENLERDE TEMEL KAVRAMLAR

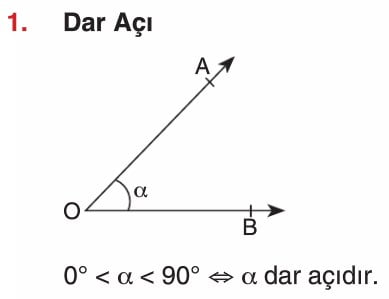
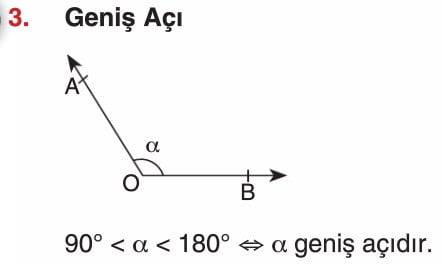
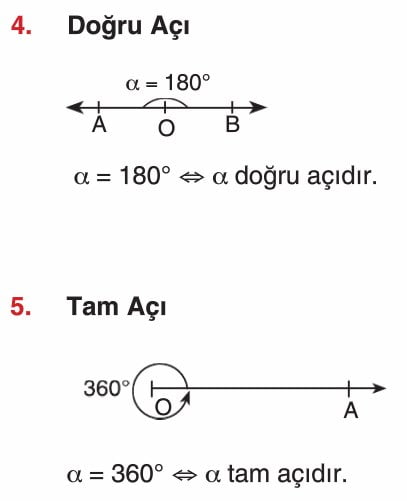
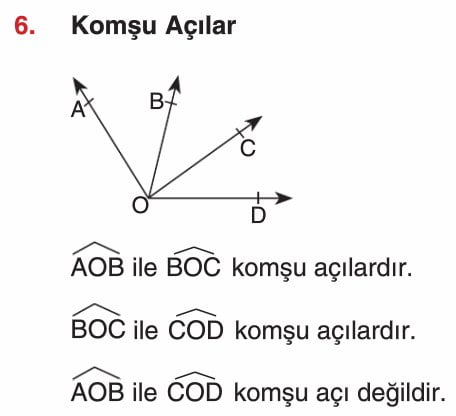
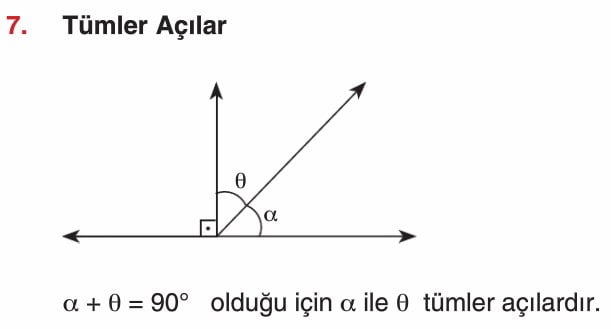
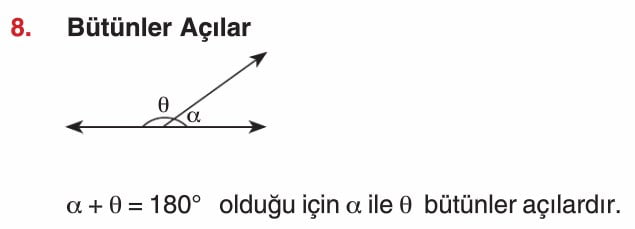
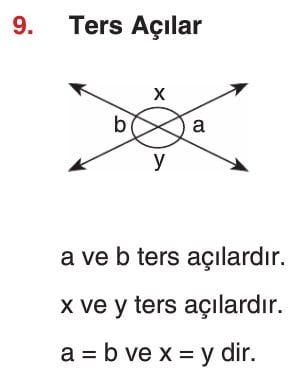
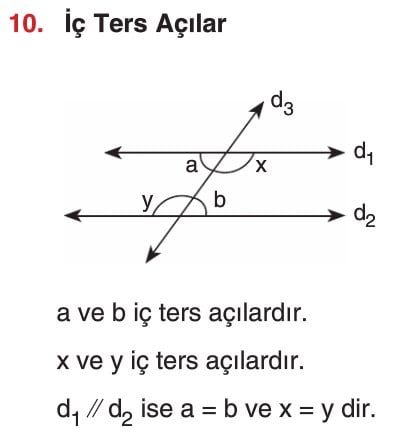
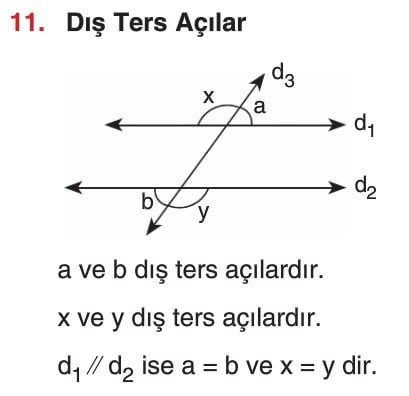
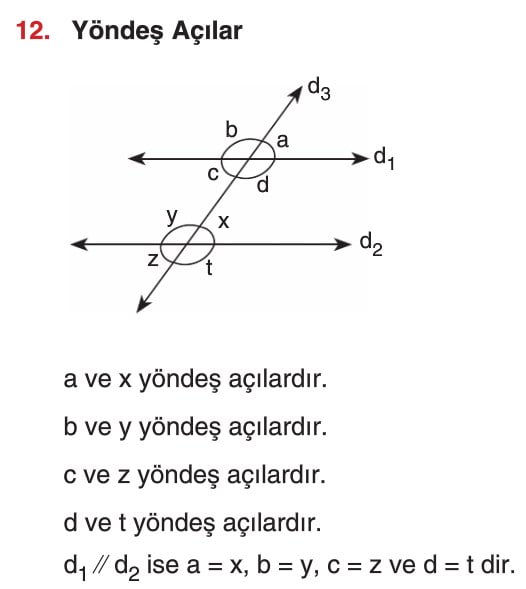
Açı Çeşitleri

---

---

---

---

Üçgen Çeşitleri

I. Açılarına Göre Üçgen Çeşitleri

II. Kenarlarına Göre Üçgen Çeşitleri

---

---

_{Üçgende Açı Özellikleri}

---

---

Üçgende Açılar Çözümlü Örnekler

---

---

Üçgen Çeşitleri
1. Kenarlarına göre üçgenler:
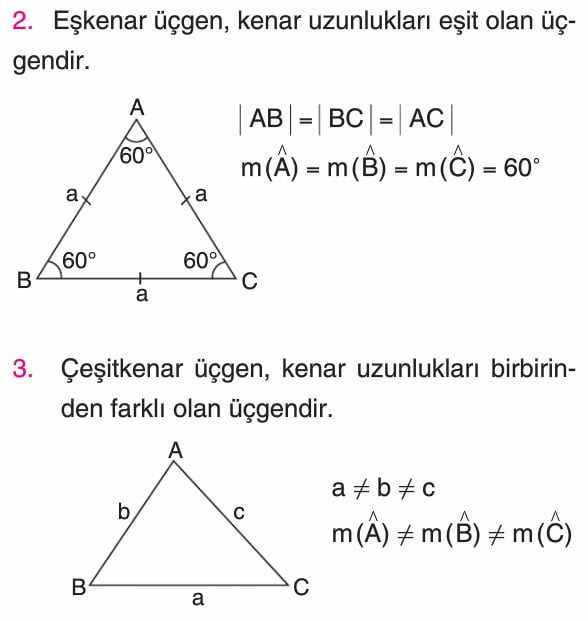
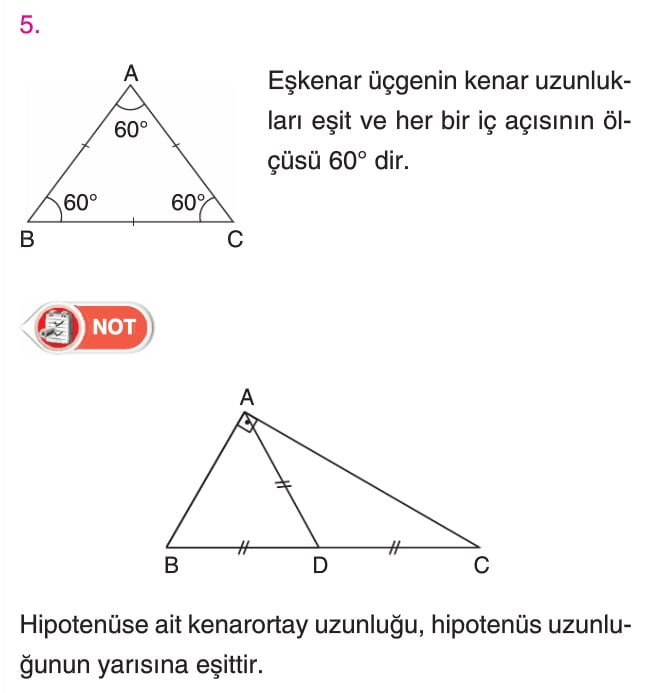
    a) Eşkenar üçge
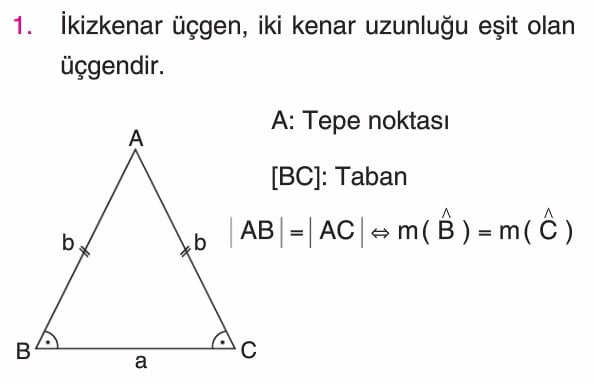
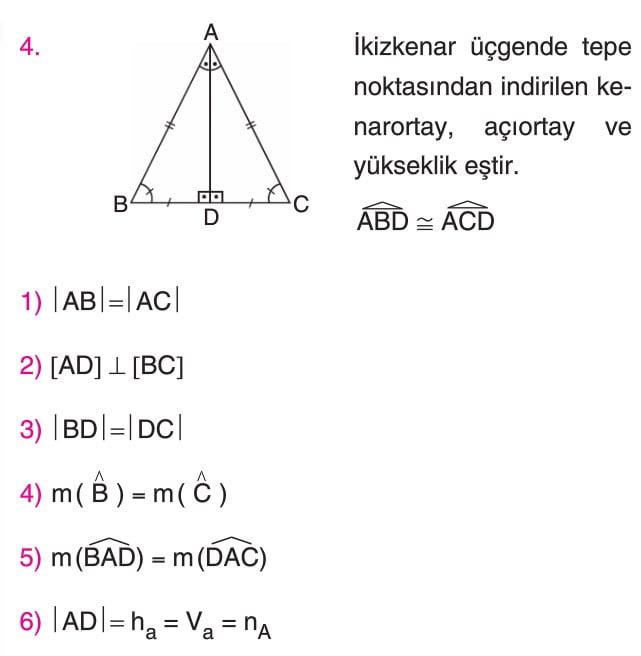
    b) İkizkenar üçgen    
    c) Çeşitkenar üçgen
2. Açılarına Göre Üçgenler
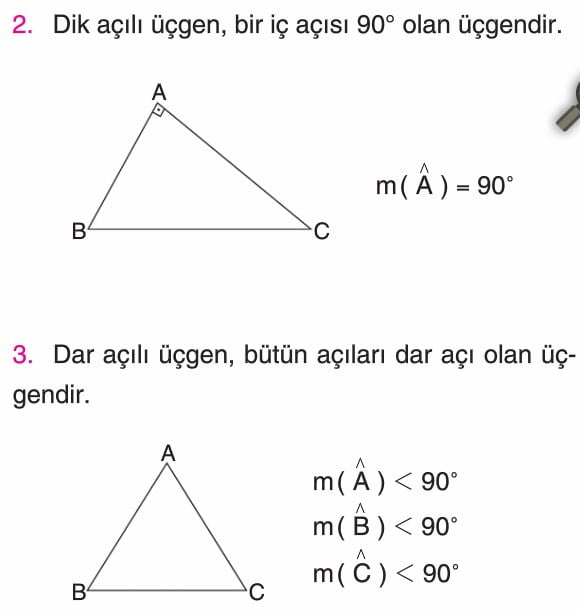
   a) Dar açılı üçgen
   b) Dik açılı üçgen
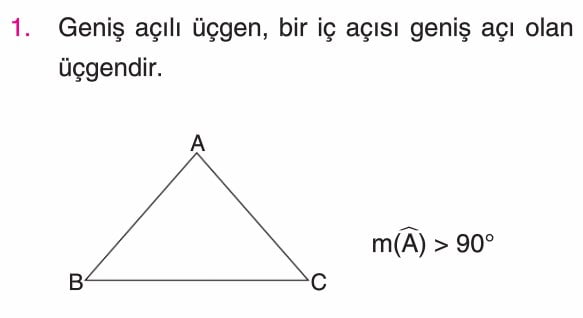
   c) Geniş açılı üçgen

Üçgenlerde Eşlik

ÜÇGENLERDE EŞLİK ŞARTLARI

İki üçgenin karşılıklı tüm kenarlarının uzunlukları ve tüm açılarının ölçüleri eşitse bu iki üçgen eştir. Ancak iki üçgenin tüm kenarları ve tüm açıları her zaman verilmeyebilir. Böyle durumlarda bu kısıtlı verilere bakarak da biz iki üçgenin eş olup olmadığına kanaat getirebiliriz. Bunun için aşağıdaki eşlik şartlarını kullanırız. Eğer iki üçgen arasında bu şartlardan biri sağlanıyorsa bu iki üçgen eştir diyebiliriz.

1) Kenar – Kenar – Kenar Eşlik Şartı (KKK)

# İki üçgen arasında birebir eşleme yapıldığında karşılıklı tüm kenar uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna;  Kenar – Kenar – Kenar (KKK) eşlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Kenar-Kenar eşlik şartına göre eştir.

2) Kenar – Açı – Kenar Eşlik Şartı (KAK)

# İki üçgen arasında birebir eşleme yapıldığında ikişer kenar uzunlukları ve bu iki kenar arasında kalan açılarının ölçüleri eşit ise bu üçgenler eş üçgenlerdir. Buna;  Kenar – Açı – Kenar (KAK) eşlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Açı-Kenar eşlik şartına göre eştir.

3) Açı – Kenar – Açı Eşlik Şartı (AKA)

# İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu iki açı arasında kalan kenar uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna;  Açı – Kenar – Açı (AKA) eşlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Açı-Kenar-Açı eşlik şartına göre eştir.

4) Kenar – Açı – Açı Eşlik Şartı (KAA)

# İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu açılardan herhangi birinin karşısındaki kenarın uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna;  Kenar – Açı – Açı (KAA) eşlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Açı-Açı eşlik şartına göre eştir.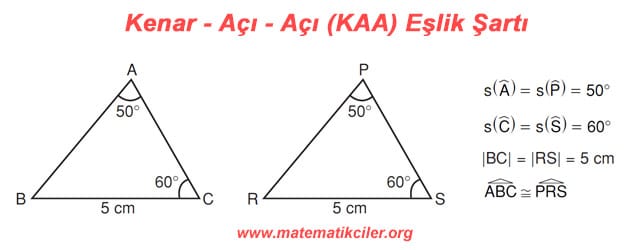 

ÜÇGENLERDE BENZERLİK

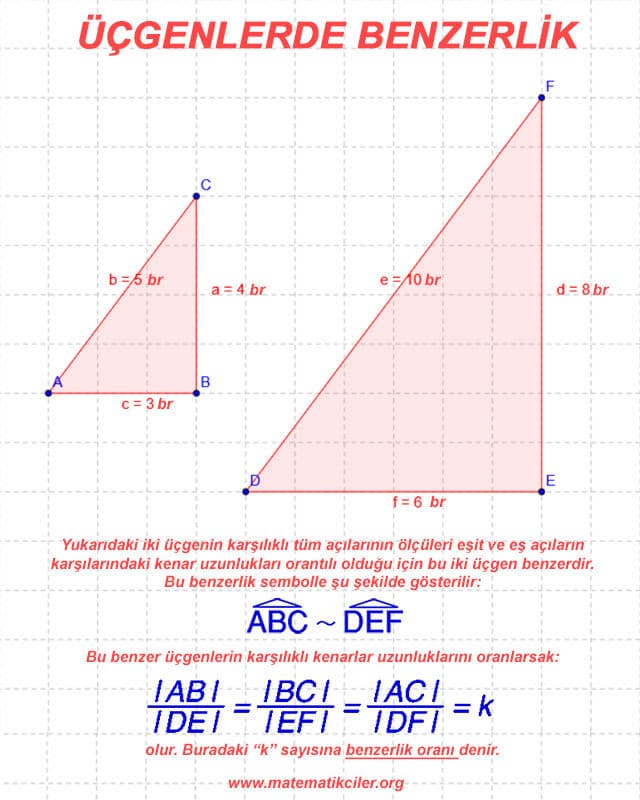
# İki üçgenin karşılıklı  açılarının ölçüleri birbirine eşit ve karşılıklı kenarlarının uzunlukları orantılı ise bu üçgenler benzer üçgenlerdir.

# İki üçgenin benzerliği “∼” sembolü ile gösterilir. Sembolle gösterirken eş olan açılar aynı sırada yazılmalıdır.

# Benzer iki üçgende karşılıklı kenarları oranlarsak bu oranlar bir sayıya eşit olur. Bu sayıya benzerlik oranı denir. Genelde k harfi ile gösterilir.

Örneğin aşağıdaki örnekte benzerlik oranı 1/2’dir. Pay ve paydaların yeri değişirse benzerlik oranı 2 olarak da yazılabilir.

Bu, “DEF üçgeninin kenar uzunlukları ABC üçgeninin 2 katıdır.” veya “ABC üçgeninin kenar uzunlukları DEF üçgeninin yarısıdır.” anlamına gelir.

ÜÇGENLERDE BENZERLİK ŞARTLARI

İki üçgenin tüm kenarları ve tüm açıları her zaman verilmeyebilir. Böyle durumlarda bu kısıtlı verilere bakarak da biz iki üçgenin benzer olup olmadığına kanaat getirebiliriz. Bunun için aşağıdaki benzerlik şartlarını kullanırız. Eğer iki üçgen arasında bu şartlardan biri sağlanıyorsa bu iki üçgen benzerdir diyebiliriz.

1) Kenar – Kenar – Kenar Benzerlik Şartı (KKK)

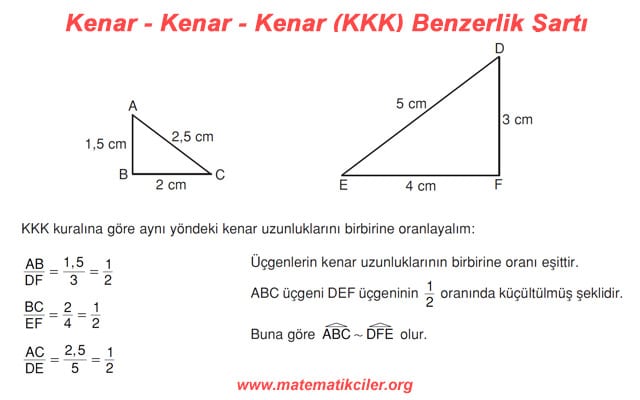
# İki üçgen arasında birebir eşleme yapıldığında karşılıklı kenar uzunluklarının oranı birbirine eşit isebu üçgenler benzer üçgenlerdir. Buna;  Kenar – Kenar – Kenar (KKK) benzerlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Kenar-Kenar benzerlik şartına göre benzerdir.

2) Kenar – Açı – Kenar Benzerlik Şartı (KAK)

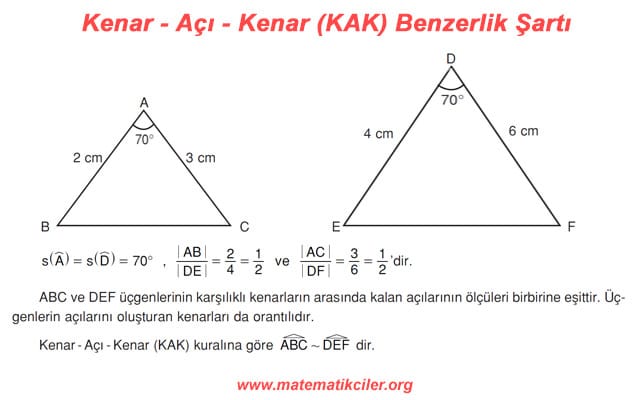
# İki üçgen arasında birebir eşleme yapıldığında karşılıklı ikişer kenar uzunluklarının oranı ve bu iki kenar arasında kalan açılarının ölçüleri birbirine eşit ise bu üçgenler benzerdir üçgenlerdir. Buna;  Kenar – Açı – Kenar (KAK) benzerlik şartı denir.

ÖRNEK: Aşağıdaki iki üçgen Kenar-Açı-Kenar benzerlik şartına göre benzerdir.

3) Açı – Açı Benzerlik Şartı (AA)

# İki üçgen arasında birebir eşleme yapıldığında karşılıklı iki açılarının ölçüleri birbirine eşit ise bu üçgenler benzer üçgenlerdir. Buna;  Açı – Açı (AA) benzerlik şartı denir. İki açıları eş olduğu için üçüncü açıları da eştir. Bu yüzden bu şarta Açı – Açı – Açı (AAA) benzerlik şartı da denilebilir.

ÖRNEK: Aşağıdaki iki üçgen Açı-Açı benzerlik şartına göre benzerdir.

EŞLİK VE BENZERLİK İLE İLGİLİ

# Her eş üçgen aynı zamanda benzerdir, ancak her benzer üçgen eş olmak zorunda değildir.

# Eş üçgenler benzerlik oranı 1 olan benzer üçgenlerdir.

# İki üçgenin benzerlik oranı k ise çevreleri oranı da k’dır.

# İki üçgenin benzerlik oranı k ise karşılıklı yükseklikleri, açıortayları, kenarortayları oranı da k’dır.

# İki üçgenin benzerlik oranı k ise alanları oranı da k2‘dir.

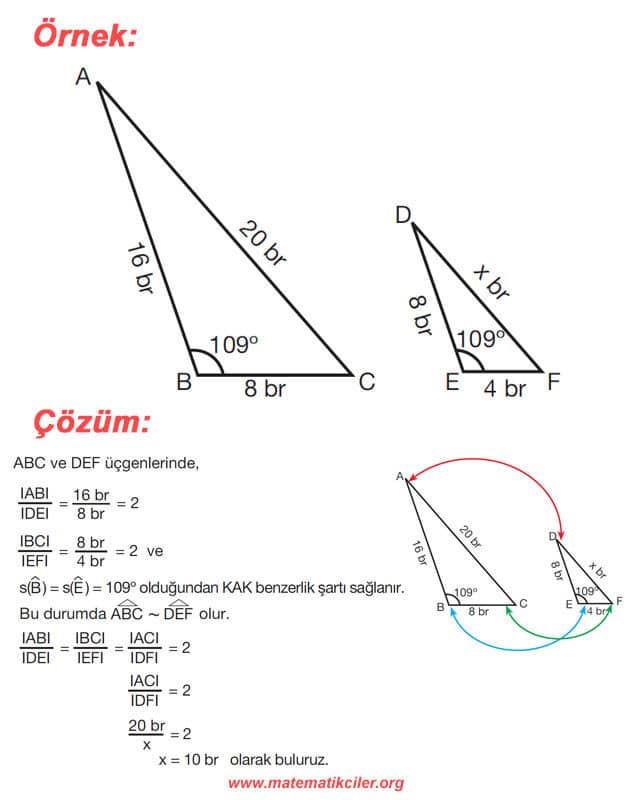
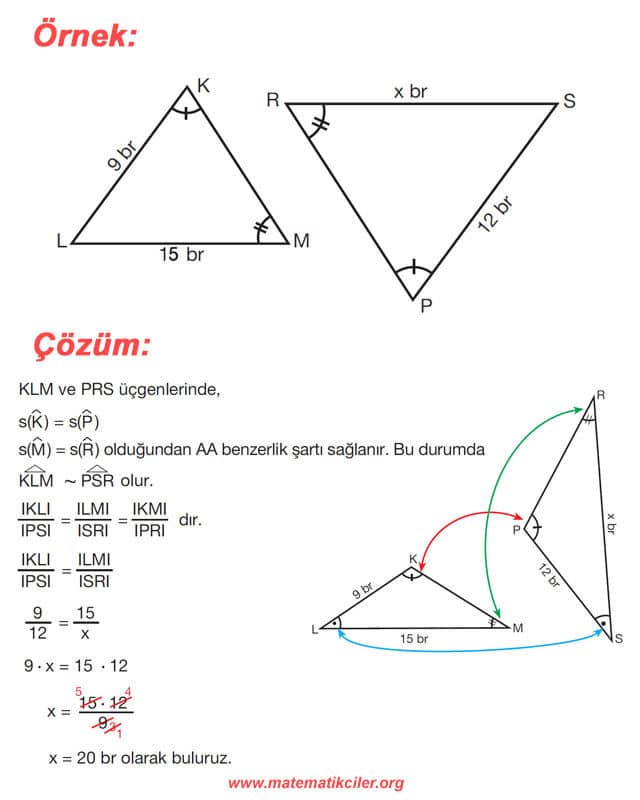
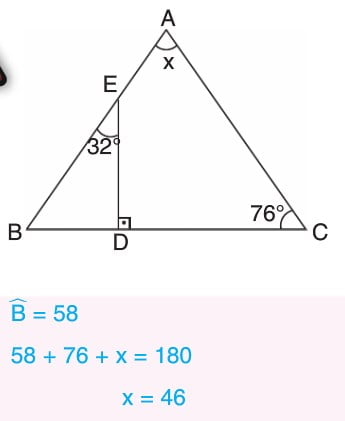
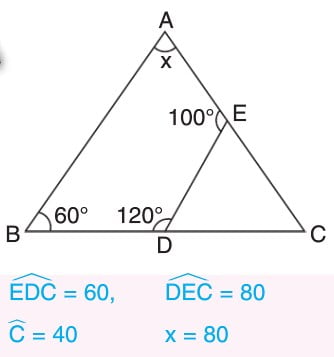
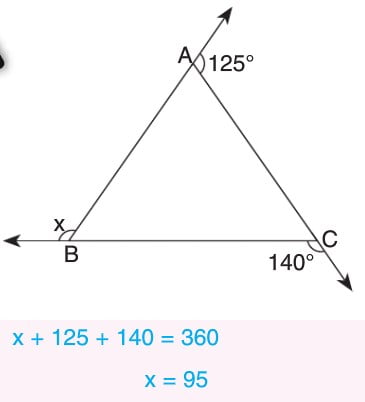
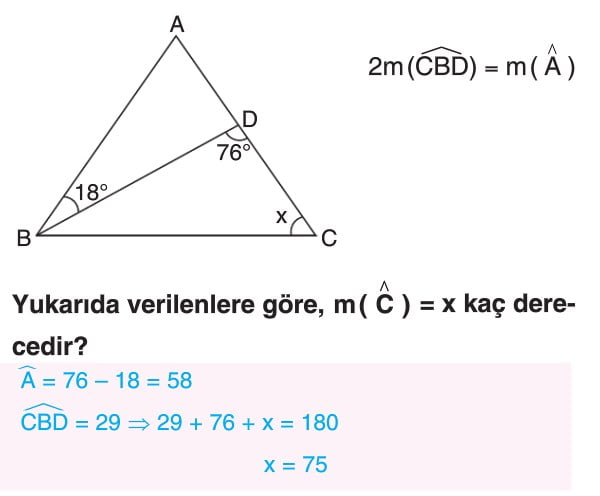
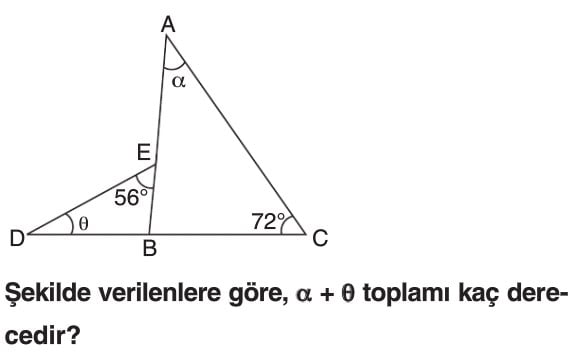
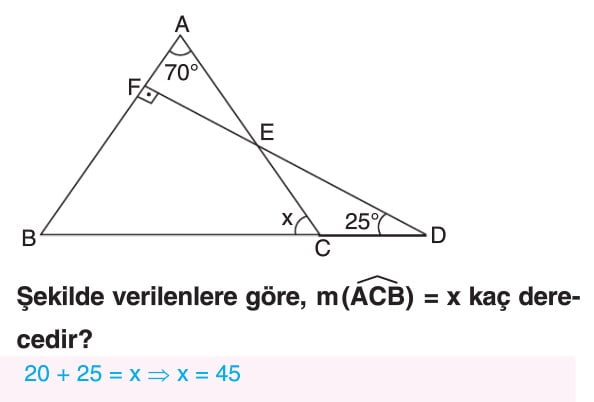
ÖRNEKLER: Aşağıdaki üçgenlerde x ile gösterilen uzunlukları bulalım.

Üçgenin Yardımcı Elemanları

0

7468

Üçgenin yardımcı elemanları Yükseklik, Açıortay, Kenarortay ve Kenar orta dikmedir. Güncellenen yeni programda 8.sınıfta kenar orta dikme konusu işlenmemektedir. Başarılar dileriz. 

1) Yükseklik

» Bir köşeden karşı kenara veya kenarın uzantısına çizilen dik doğru parçasına yükseklik denir.» Bir üçgende  üç farklı yükseklik çizilebilir.» Bir üçgende yüksekliklerin kesiştiği noktaya Diklik Merkezi denir.» Bir üçgende a kenarına çizilen yükseklik sembolle ha  şeklinde gösterilir.
» Yandaki gibi dar açılı üçgenlerde çizilen yükseklikler üçgenin iç bölgesinde olur.» Dar açılı üçgenlerde diklik merkezi üçgenin iç bölgesinde bulunur.

 

» Yandaki gibi geniş açılı üçgenlerde çizilen yüksekliklerden bir tanesi üçgenin iç bölgesinde, iki tanesi ise üçgenin dış bölgesinde bulunur.» Geniş açılı üçgenlerde diklik merkezi üçgenin dış bölgesinde bulunur.

NOT: Dik açılı üçgenlerde üçgenin üç yüksekliğinden ikisi zaten çizilidir, dik kenarlar üçgenin aynı zamanda yüksekliğidir. Diğer yükseklik ise dik açının bulunduğu köşeden hipotenüse çizilir. Dik açılı bir üçgende diklik merkezi üçgenin üzerindedir, dik açının bulunduğu köşe üçgenin üç yüksekliğinin kesiştiği noktadır.

2) Açıortay

» Üçgenin herhangi bir köşesindeki açıyı iki eş parçaya bölen ışına o açının açıortayıdenir.

» A köşesine ait açıortay sembolle nA şeklinde gösterilir.

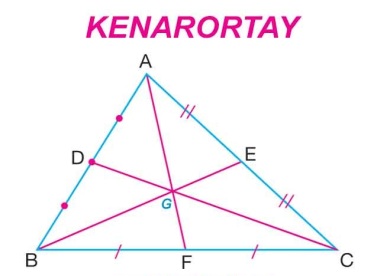
3) Kenarortay

» Bir üçgende bir kenarın orta noktasını karşısındaki köşeye birleştiren doğru parçasına kenarortay denir.

» a kenarına ait kenar ortay sembolle Va şeklinde gösterilir.

» Bir dik üçgende hipotenüse ait kenar ortay hipotenüs uzunluğunun yarısına eşittir

DİK ÜÇGENDEKİ ORANLAR

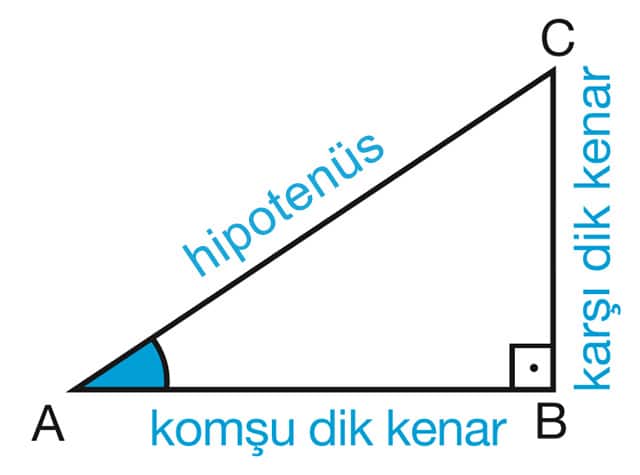Dik üçgende 90 derece dışındaki diğer açılardan birini seçelim. Örneğin resimde A açısı seçilmiştir.
Trigonometrik oranları yazarken resimdeki gibi bir isimlendirme kullanacağız. 90 derecenin karşısındaki kenara hipotenüs, seçtiğimiz açının karşısındaki kenara karşı kenar, geriye kalan ve açının bir kolu olan kenara ise komşu kenar diyeceğiz. İsimlendirme işinde de anlaştığımıza göre gelelim bu kenarları oranlamaya.

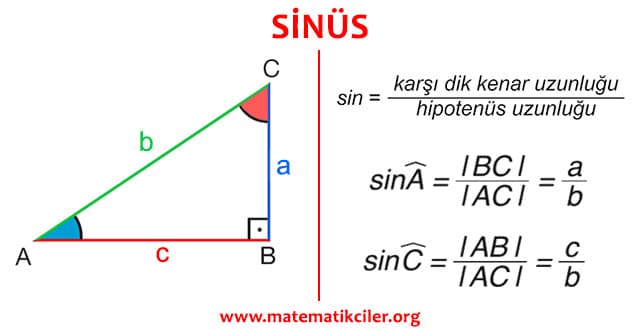
SİNÜS

Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının sinüsü denir. Bir A açısının sinüsü “sin A” şeklinde gösterilir.

KOSİNÜS

Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının kosinüsü denir. Bir A açısının kosinüsü “cos A” şeklinde gösterilir.

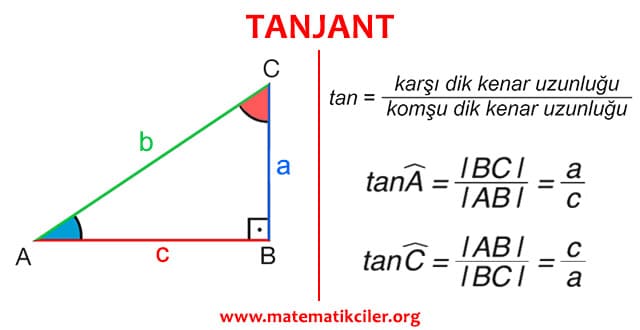
TANJANT

Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun komşu dik kenar uzunluğuna oranına o dar açının tanjantı denir. Bir A açısının tanjantı “tan A” şeklinde gösterilir.

KOTANJANT

Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun karşısındaki dik kenar uzunluğuna oranına o dar açının kotanjantı denir. Bir A açısının kontanjantı “cot A” şeklinde gösterilir.

 ÇIKARILACAK DERSLER

Yukarıdaki trigonometrik oranları incelediğinizde aşağıdaki yazılanların bazılarını (belki hepsini) keşfetmiş olabilirsiniz. Ama biz yine de yazalım.
# Birbirini 90 dereceye tamamlayan (birbirinin tümleri olan) iki açıdan birinin sinüsü, diğerinin kosinüsüne eşittir.
# Birbirini 90 dereceye tamamlayan (birbirinin tümleri olan) iki açıdan birinin tanjantı, diğerinin kotanjantına eşittir.
# Bir dar açının tanjantı ile kotanjantı birbirinin çarpmaya göre tersidir. (Çarpmaya göre tersi?)
“Komşu/Hipotenüs Sinüs müydü, Kosinüs müydü?” veya “Komşu / Karşı Tanjant mıydı, Kotanjant mıydı?” gibi sorulara çözüm olarak şöyle bir yöntem izleyebilirsiniz. “Ko” ile başlayanların (yani kosinüs ve kotanjant) payında komşu var.

ÖZEL DİK ÜÇGENLERDE TRİGONOMETRİK ORANLAR

30 – 60 – 90 ÜÇGENİ

Eşkenar üçgende bir kenara ait yükseklik çizilirse oluşan iki dik üçgenin de açıları 30° – 60° – 90° olur. Bu eşkenar üçgenin bir kenarının uzunluğunu 2a kabul edersek, oluşan dik üçgenlerde 30 derecelik açının karşısı a olur çünkü yükseklik aynı zamanda kenarortaydır. Yüksekliğin uzunluğunu da Pisagor Bağıntısından bulabiliriz. Bu kenarları oranlarsak aşağıdaki trigonometrik oranları elde ederiz.

Buradan şu sonuçlara da varabiliriz. 30-60-90 üçgeninde:
# Hipotenüsün uzunluğu 30 derecelik açının karşısındaki kenarın uzunluğunun 2 katıdır.
# 60 derecelik açının karşısındaki kenarın uzunluğu, 30 derecelik açının karşısındaki kenarın uzunluğunun 3–√$\sqrt{3}$ katıdır.

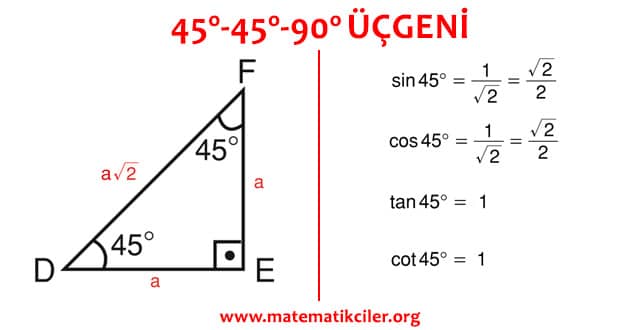
45- 45 – 90 ÜÇGENİ

İkizkenar bir dik üçgenin açıları 45° – 45° – 90° ‘dir. Bu ikizkenar dik üçgenin dik kenarlarının uzunluğunu a kabul edersek hipotenüsün uzunluğunu Pisagor Bağıntısından a2–√$a\sqrt{2}$ buluruz. Bu kenarları oranlarsak aşağıdaki trigonometrik oranları elde ederiz.

Buradan şu sonuca da varabiliriz. 45-45-90 üçgeninde:
# Hipotenüsün uzunluğu diğer kenarların uzunluğunun 2–√$\sqrt{2}$ katıdır.

30° – 45° – 60° AÇILARININ TRİGONOMETRİK ORAN TABLOSU

Üçgenin Alanı Nasıl Bulunur?

30.03.2018 - 20:40

Üçgen geometrinin temelidir. Üçgenin alanını hesaplayabilmek, geometrideki bütün alan sorularını yapmanın anahtarıdır. Bu nedenle bu yazıda üçgenin alanı nasıl bulunur onun üzerinde duracağız. 6. sınıf matematik dersinden başlayarak bütün eğitim hayatımız boyunca üçgenin alanı bize çok lazım olacaktır.

Bu nedenle konuyu iyi öğrenmeye özen göstermeliyiz. Öncelikle belirtelim ki üçgenin alanını hesaplamak geometrideki en kolay şeydir. Basit bir formülü uygulamak yetecektir.

Konuyu detaylıca öğrenmek isteyenler için üçgenin alanı adlı konu anlatımını hazırladık. Vakti olmayanlar için basitçe üçgenin alanı formülünü verelim.

Üçgenin Alanı Formülü

Üçgenin alanının bir tane formülü vardır. Kenar x yükseklik / 2 formülüyle üçgende alan sorularını kolaylıkla ve yapabilirsiniz. Burada dikkat etmeniz gereken en önemli şey yüksekliğin o kenara ait olmasıdır. Üçgen içerisinde herhangi bir kenarı seçip o kenara ait yükseklikle çarpıp ikiye bölüyorsunuz.

Üçgenin kenarına a ve a kenarına ait yüksekliğe h dersek, alan formülü Alan = a.h / 2 olur.

Yukarıdaki görselde üçgenin alanı formülü verilerek basitçe ne işlem yapacağımız görselleştirilmiştir.

Şunu belirletim ki dik üçgende zaten iki kenar birbirine dik olduğu için dik kenarları çarpıp ikiye bölmek yeterlidir. İçeriden ekstra bir yükseklik çizmeye gerek yoktur. Basit bir örnek yapalım.

Örnek: Aşağıdaki resimde 3m ve 4m şeklinde uzunluğu verilen üçgenin alanı kaç m2 olur?

Çözüm: Çok basit. Dik kenarları çarparız ve ikiye böleriz. 3.4 / 2 = 12 / 2 = 6 m2 olur.

Eşkenar Üçgenin Alanı Nasıl Bulunur?

Yukarıda verdiğimiz formülle bütün alan soruları çözülebilir. Ancak özel üçgenlerde bize yükseklik vermeyebilir. Bu durumda yüksekliği kendimiz çizip Pisagor bağıntısıyla bulmamız gerekecektir.

Eşkenar üçgende üç kenar uzunluğu da eşit olduğu için, üç kenara ait yüksekliklerin uzunluğu eşittir. Aynı zamanda kenar uzunluğu ile yükseklik arasında da sabit bir oran vardır. Bu nedenle sadece bir kenarı bilinen bir eşkenar üçgenin alanı rahatlıkla bulunabilir.

Kenar uzunluğu a olan bir eşkenar üçgenin alanı formülü Alan = a2.√3 / 4 şeklindedir.

Yani bir kenar uzunluğu 8 cm olan bir üçgenin alanı 64.√3 / 4 = 16√3 cm2 olacaktır.

İkizkenar Üçgenin Alanı Nasıl Bulunur?

İkizkenar üçgen iki kenar uzunluğu eşit olan üçgendir. Üçgenin üçüncü kenarının ise uzunluğu farklıdır.

Eğer üç kenar uzunluğu da verilmişse o zaman uzunluğu farklı olan kenara yükseklik çizilir. Çizilen yükseklik aynı zamanda kenarortay da olacağına göre kenarı iki eş parçaya ayıracaktır. Bu durumda Pisagor bağıntısı kullanılarak yükseklik bulunur. Ardından da formül uygulanır.

Not: Yüksekliğin verilmediği durumlarda yüksekliği kendimiz çizip Pisagor bağıntısı ile uzunluğunu hesaplamalıyız.

Çeşitkenar Üçgenin Alanı

Çeşitkenar üçgen üç kenar uzunluğu da farklı olan üçgendir. Çeşitkenar üçgenin alanını hesaplamak için herhangi bir kenarın uzunluğunu ve o kenara ait yüksekliği bilmemiz yeterlidir. Yukarıda verdiğimiz formül bütün üçgenler için geçerlidir.

Fakat çeşitkenar üçgenin üç kenar uzunluğunu da bilmemize rağmen herhangi bir yükseklik bilmiyorsak o zaman alanı bulmak için şu adımları takip ederiz:

1. Üçgenin üç kenarını toplayarak çevresini bul. (Üçgenin alanı nasıl bulunur biliyorsunuz zaten.)
2. Bulduğun çevreyi ikiye böl ve çıkan sonucu bir harfe eşitle. (Mesela u harfi olsun.)
3. Kenarları a, b, c olan üçgen için Alan = √(u(u-a)(u-b)(u-c)) formülünü uygula.

Bir örnekle pekiştirelim. Kenar uzunlukları 6, 8 ve 10 cm olan üçgenin alanını bulalım.

Çevreyi 6 + 8 + 10 = 24 cm olarak buluruz. Çevrenin yarısı 24 / 2 = 12'dir. (u = 12)

Öyleyse alan = √(12(12-6)(12-8)(12-4)) = √(12.6.4.8) = √2304 = 48 cm2 bulunur.