Sayma Sayıları
SAYI KÜMELERİ
Dik kenar uzunlukları 1'er cm olan olan bir dik üçgenin hipotenüs uzunluğunu veya bir tekerleğin çevresini bulmak için rasyonel sayılardan daha geniş sayı kümelerine gereksinim vardır. Bu bölümde ortaokul yıllarından öğrendiğiniz doğal sayılar kümesi, tam sayılar kümesi ve rasyonel sayılar kümesi üzerinde kısaca durup irrasyonel sayılar kümesinden bahsedeceğiz. En sonunda ise bu sayı kümelerini kapsayan gerçek (reel) sayılar kümesini inceleyeceğiz.
Sayıları ifade etmeye yarayan (O, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarına rakam denir. Doğal sayıları oluşturan rakamlar birler, onlar, yüzler… basamağı gibi basamak değerlerine sahiptir. Sayıların basamak değerlerinin toplamı olarak yazılmasına çözümleme denir.
2 nin katı olan tam sayılara çift sayı, 2 nin katı olmayan tam sayılara tek sayı denir.
Tek sayıları T, çift sayıları Ç ile gösterirsek
Ç = {… -4, -2, 0, 2, 4, …)
T = {… -3, -1, 1, 3, …) olur.
Ç = {… -4, -2, 0, 2, 4, …)
T = {… -3, -1, 1, 3, …) olur.
Bir çarpımın sonucu tek sayı ise çarpılan bütün sayılar tektir.
Bir çarpımın sonucu çift sayı ise çarpılan sayılardan en az bir tanesi çifttir.
Bir çarpımın sonucu çift sayı ise çarpılan sayılardan en az bir tanesi çifttir.
Sayma Sayıları Kümesi (N+ )
N+ = S = {1, 2, 3, ….. }
N+ = S = {1, 2, 3, ….. }
Doğal Sayılar Kümesi (N)
N = {0, 1, 2, 3, ….. }
N = {0, 1, 2, 3, ….. }
Tam Sayılar Kümesi (Z)
Z– = {…, –3, –2, –1} negatif tam sayılar kümesi, Z+ = {1, 2, 3, … } pozitif tam sayılar kümesidir.
Z = Z– ∪ {0 } ∪ Z+ = {…, –3, –2, –1, 0, 1, 2, 3, … }
Z– = {…, –3, –2, –1} negatif tam sayılar kümesi, Z+ = {1, 2, 3, … } pozitif tam sayılar kümesidir.
Z = Z– ∪ {0 } ∪ Z+ = {…, –3, –2, –1, 0, 1, 2, 3, … }
Rasyonel Sayılar Kümesi (Q)
Q = { a / b : a ∈ Z, b ∈ Z ve b ≠ 0 }
Q = { a / b : a ∈ Z, b ∈ Z ve b ≠ 0 }
İrrasyonel Sayılar Kümesi (Q′ )
Rasyonel olmayan sayılar kümesidir. kök 2, kök 3 , π , e , … gibi
Rasyonel olmayan sayılar kümesidir. kök 2, kök 3 , π , e , … gibi
Reel (Gerçel) Sayılar Kümesi (R)
Rasyonel sayılarla irrasyonel sayıların birleşimine reel (gerçel) sayılar kümesi denir.
Rasyonel sayılarla irrasyonel sayıların birleşimine reel (gerçel) sayılar kümesi denir.
Bölünebilme Kuralları
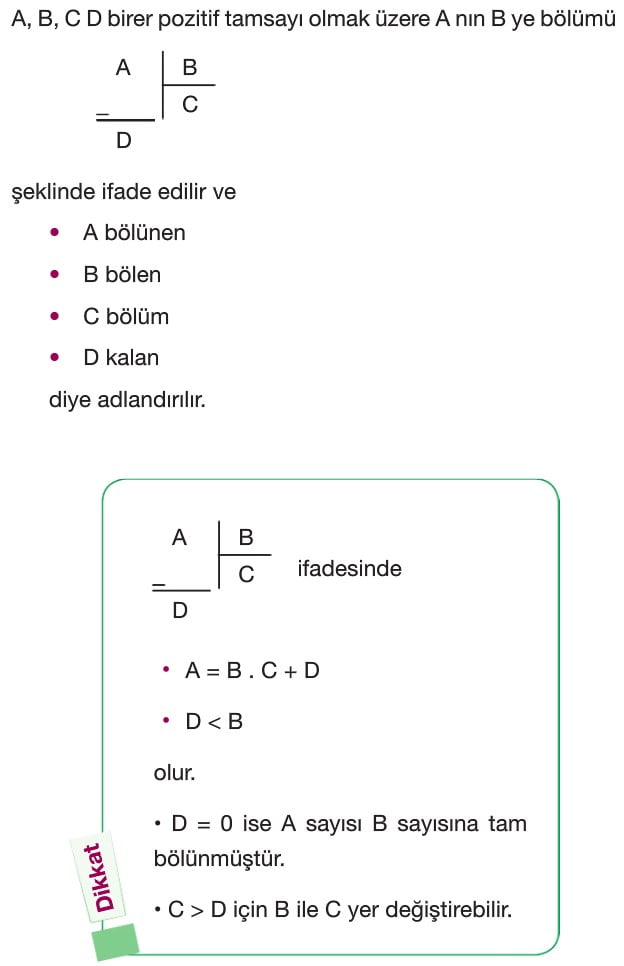
A) Bölme
B) Bölünebilme Kuralları
2 ile Bölünebilme Kuralı
3 ile Bölünebilme Kuralı
4 ile Bölünebilme Kuralı
5 ile Bölünebilme Kuralı
8 ile Bölünebilme Kuralı
9 ile Bölünebilme Kuralı
10 ile Bölünebilme Kuralı
11 ile Bölünebilme Kuralı
C) Aralarında Asallık
İki doğal sayıyı ortak olarak bölen 1 ‘den başka pozitif tamsayı yoksa bu iki sayı aralarında asaldır. Bu durum ikiden fazla sayı içinde geçerlidir.
Örneğin; 4 ile 15 sayıları 1 den başka bir pozitif tam sayıya ortak olarak bölünemez. Aralarında asaldırlar.
Örneğin; 2, 6, 15 sayıları aralarında asaldır.
Örneğin; 4 ile 15 sayıları 1 den başka bir pozitif tam sayıya ortak olarak bölünemez. Aralarında asaldırlar.
Örneğin; 2, 6, 15 sayıları aralarında asaldır.
Dikkat: Ardışık iki pozitif tamsayı daima aralarında asaldır.
Örneğin; 3 ve 4 gibi
Örneğin; 5 ve 6 gibi
Örneğin; 3 ve 4 gibi
Örneğin; 5 ve 6 gibi
Aralarında Asal Çarpanlarının Oluşturduğu Sayıya Bölünebilme
a ve b aralarında asal olsun. a . b`ye bölünebilen bir sayı hem a’ya, hem de b’ye bölünebilir.
Örneğin; 15’e bölünebilen bir sayı 3 ve 5 ile de bölünebilir.
Örneğin; 18’e bölünebilen bir sayı 2 ve 9 ile de tam bölünebilir.
Örneğin; 15’e bölünebilen bir sayı 3 ve 5 ile de bölünebilir.
Örneğin; 18’e bölünebilen bir sayı 2 ve 9 ile de tam bölünebilir.
D) Ebob Ekok
Asal Çarpanlara Ayırma
EBOB
x ve y en az biri sıfırdan farklı doğal sayılar olmak üzere “Hem x’i, hemde y’yi ortak bölen pozitif tamsayıların en büyüğü” en büyük ortak bölendir.
EBOB (x, y) veya (x, y)EBOB şeklinde gösterilir.
Örneğin; 12 ve 18’i ortak bölen değerler 1, 2, 3, 6 değerleridir. Bunların en büyüğü 6’dır. O halde EBOB (12, 18) = 6
Dikkat: EBOB’unun bulunması istenilen sayılar büyüdükçe tek tek yazarak bakmak zordur. Bu durumda sayıları asal çarpanlara ayırarak EBOB bulunur. BÖLEN ve ÇARPAN kavramlarının aynı olduğunu unutmayalım.
EKOK
Ebob Problemleri
Ekok Problemleri
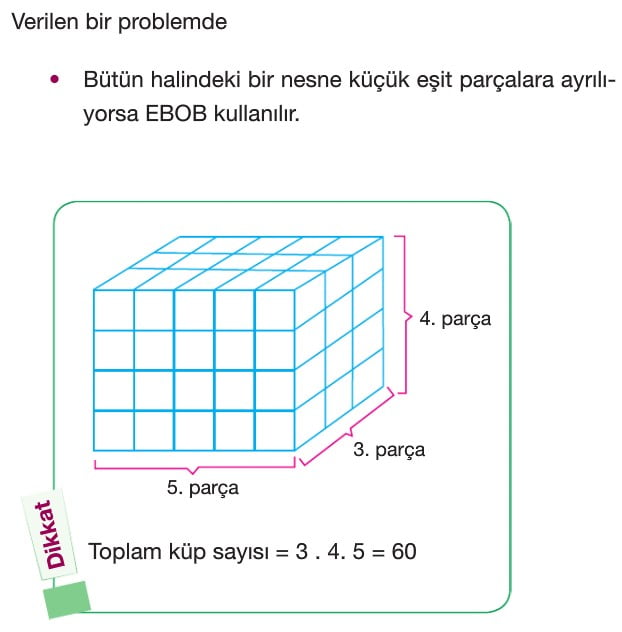
Verilen bir problemde verilen eşit parçalar birleştirilerek bütün oluşturulacaksa EKOK kullanılır.
Dikkat: x, y, z birer pozitif tamsayı olmak üzere, bir sayı
- hem x in katı
- hem y nin katı
- hem z in katı
oluyorsa bu sayının alabileceği en küçük pozitif tamsayı değeri
EKOK (x, y, z) dir.
EKOK (x, y, z) dir.
Örneğin; A = 4x = 5y = 6z ise A nın en küçük pozitif tamsayı değeri
EKOK (4, 5, 6) = 60 olur.
EKOK (4, 5, 6) = 60 olur.
Birinci Dereceden Denklemler ve Eşitsizlikler
Neler öğreneceksiniz?• Açık, kapalı, yarı açık aralık kavramları ve bunların gösterimleri ile işlemler yapma,
• Birinci dereceden bir bilinmeyenli denklemlerin çözümünü gerçek hayat durumlarını içeren problemlerde kullanma,
• Mutlak değer kavramını, mutlak değer içeren denklem ve eşitsizliklerin çözüm kümelerini bulma,
• Birinci dereceden iki bilinmeyenli denklem ve eşitsizlik sistemlerinin çözümünü analitik düzlemde yorumlama.
• Birinci dereceden bir bilinmeyenli denklemlerin çözümünü gerçek hayat durumlarını içeren problemlerde kullanma,
• Mutlak değer kavramını, mutlak değer içeren denklem ve eşitsizliklerin çözüm kümelerini bulma,
• Birinci dereceden iki bilinmeyenli denklem ve eşitsizlik sistemlerinin çözümünü analitik düzlemde yorumlama.
• 2a + 8
• 5x 12
• x2 + 3x 2
ifadeleri birer cebirsel ifadedir ve denklem belirtmez.
• 5x 12
• x2 + 3x 2
ifadeleri birer cebirsel ifadedir ve denklem belirtmez.
- a ve b gerçek sayılar ve a ≠ 0 olmak üzere, ax + b = 0 şeklindeki ifadelere birinci dereceden bir bilinmeyenli denklem denir. Bu eşitliği sağlayan x sayısına denklemin kökü denir. Bir denklemin kökünün (veya köklerinin) oluşturduğu kümeye de çözüm kümesi denir.
El Harezmi
Türk kökenli matematik ve astronomi bilginidir. Cebir ve astronomi ile ilgili önemli eserler yazmıştır. Doğu ve batı dünyasında cebire yaptığı katkılarla ün yapıp, tanınan Harezmi, bu sahada ilk eser sahibidir. Eserlerinde Avrupa’nın bilmediği “Sıfır” ı kullanıp, cebir işlemlerini geometrik yaklaşımlarla temellendirmiştir. Harezmi ”Kitab’ül Muhtasar fi Hesabil Cebri Mukabele” adlı eseriyle “Cebir” kelimesini matematiğe kazandırarak cebir konularını metodik ve sistematik olarak ilk defa ortaya koymuştur. Latince’ye çevrilip Avrupa’da yüzyıllarca kullanılan bu kitap, Amerika’da da yayınlanmıştır. Eser, bir ön söz, beş bölüm ve bir de ek bölümden meydana gelmektedir. İçerik olarak, birinci ve ikinci dereceden denklemlerin çözüm şekillerini, bilinmeyenleri, çeşitli cebir hesaplamalarını, teorik ve uygulamalı hesaplamaları, zamanın hükumet işlerine ait hesaplamaları kapsamaktadır. Kitapta kanal açılması, ev ve bina yapımı ile ilgili temel hesaplamalar vardır, Harezmi’nin ikinci önemli eseri “kitab-el Muhtasar i hisaballindi” isimli kitabıdır. Kitabın Arapça aslı mevcut değildir. Kitap Cambridge Üniversitesi kütüphanesinde “Algoritmi de numero indorom” ismiyle bulunmaktadır.
Üslü İfadeler ve Denklemler
Gerçek Sayıların Tam Kuvvetleri
a bir gerçek sayı ve n bir pozitif tam sayı olmak üzere,
olacak şekilde n tane a nın çarpımı olan an ifadesine üslü sayı denir. Burada a taban, n ise kuvvetya da
üs olarak isimlendirilir. Örneğin 5 sayısının kendisi ile 3 kez çarpımı
5.5.5 = 53 olarak gösterilir.
üs olarak isimlendirilir. Örneğin 5 sayısının kendisi ile 3 kez çarpımı
5.5.5 = 53 olarak gösterilir.
Üslü sayılarda taban negatif gerçek sayı ise üst tek sayı olduğunda sonuç negatif, üs çift sayı olduğunda sonuç pozitiftir. Ancak, sonucun pozitif olması için çift kuvvetin (üssün) parantezin dışında olması gerekir.
(-2)4 = 16 iken (-24) = -16 dır.
(-2)4 = 16 iken (-24) = -16 dır.
Bir Gerçek Sayının Negatif Kuvveti
Üslü Sayılarda Toplama ve Çıkarma İşlemi
Üslü sayılar arasında toplama ve çıkarma yapılabilmesi için bu Üslü sayıların hem tabanları, hem de üsleri eşit olmalıdır.
a, b, c, x ∈ R ve m ∈ Z olmak üzere,
a.xm + b.xm – c.xm = (a + b – c).xm dir.
a.xm + b.xm – c.xm = (a + b – c).xm dir.
Üslü Sayılarda Çarpma ve Bölme İşlemi
- x ∈ R ve a, b ∈ Z olmak üzere,
xa . xb = xa+b dir.Tabanları eşit olan Üslü ifadeler çarpılırken üsler toplanır ve ortak tabanın üssü olarak yazılır.
Örneğin;
28 . 25 = 28+5 = 2133m . 38 = 3m+8
- x, y ∈ R ve a ∈ Z+ olmak üzere,
xa . ya = (x . y)a dır.
Üstleri eşit olan ifadeler çarpılınca tabanlar çarpılır, ortak üs çarpıma üs olarak yazılır.
Örneğin;
25 . 35 = (2 . 3)5 = 65 tir.
- x ∈ R, x ≠ 0 ve a, b ∈ Z olmak üzere,
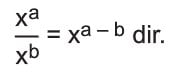
Tabanları eşit olan üslü ifadeler bölünürken, taban aynı kalır, üsler
çıkarılır.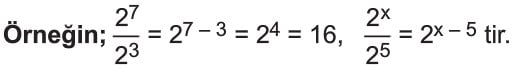
- x, y ∈ R, y≠0 ve a∈Z+ olmak üzere,
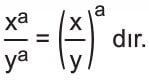 Üsleri eşit olan üslü ifadeler bölünürken tabanlar bölünür ve üs değişmeden kalır.
Üsleri eşit olan üslü ifadeler bölünürken tabanlar bölünür ve üs değişmeden kalır.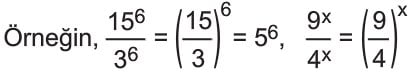
Üslü İfadelerle İlgili Bazı Özellikler
Üslü İfade İçeren Denklemler
x ∈ R-{-1,0,1} ve m, n ∈ R-{0} olmak üzere
xm = xn ise
m = n dir.
Üslü denklemlerde eşitliğin her iki tarafında tabanlar eşit ise üsler de eşittir.
xm = xn ise
m = n dir.
Üslü denklemlerde eşitliğin her iki tarafında tabanlar eşit ise üsler de eşittir.
Günlük hayatta karşılaşılan bazı problemlerin somutlaştırılıp matematik dilinde yazılması denklemler ve eşitsizlikler yardımıyla gerçekleştirilebilir. Böylece bir problemin anlaşılması, yorumlanması ve çözüme ulaştırılması oldukça kolaylaşır. Örneğin alışveriş sırasında aynı ürünün farklı miktarlarda sunulan satışının hangisinin daha hesaplı olduğu, belirlediğiniz bütçemize uygun telefon veya internet kullanımını belirlemede, ödemelerinizdeki vergi tutarlarını hesaplama gibi bir çok durumda yol gösterici olurlar. Denklem ve eşitsizlik kurma yalnızca matematiğin değil diğer birçok bilim dalının da dünyada ve evrende gerçekleşen durumları anlatmada sıkça kullandığı bir yöntemdir.
Denklem ve Eşitsizlikler konusu 9. sınıf matematik müfredatında kümeler konusundan hemen sonra gelir. Ygs Matematik sınavında Denklem ve eşitsizlikler konusundan her sene 5-6 tane soru gelmektedir. Ayrıca denklemler matematiğin en temel konusu olduğu için oldukça önemlidir.
olmak üzere,
şeklindeki ifadelere birinci dereceden bir bilinmeyenli eşitsizlik adı verilir. Eşitsizliği çözmek için f(x) = ax + b fonksiyonunun tablosu yapılır. Eşitsizliği sağlayan aralık bulunur.
f(x) = ax + b fonksiyonunun işaret tablosu aşağıda verilmiştir.
ax + b = 0 denkleminin kökü  dır.
dır.

B. KISA YOLDAN FONKSİYONUN İŞARETİNİN İNCELENMESİ
Kısalığından dolayı bütün eşitsizliklerin çözüm yolunu kolayca bulabileceğiniz bir yaklaşım vereceğiz.
f(x), çarpım veya bölüm fonksiyonu olsun.
Tablo oluştururken sırasıyla şu işlemler yapılır:
1) f(x) in payı ile paydasını sıfır yapan değerler bulunup sırasıyla tabloya yazılır.
2) (Eşitsizliğin tanımı gözönüne alınarak) pay ile paydayı sıfır yapan değerlerden tek sayıda olanlarına tek katlı kök, çift sayıda olanlarına çift katlı kök denir.
3) Her bileşenin en büyük dereceli terimlerinin işaretleri çarpılarak veya bölünerek f(x) in işareti bulunur.
4) Tablodaki en büyük kökün sağındaki kutuya f(x) in işareti yazılır.
5) Tek katlı köklerin soluna sağındaki işaretinin tersi, çift katlı köklerin soluna sağındaki işaretin aynısı yazılır.
Kural
Uyarı
 gibi eşitsizliklerin çözüm kümesi bulunurken, içler dışlar çarpımı yapılamaz. Çünkü paydadaki f(x), h(x) ve m(x) in pozitif ya da negatif olduğunu bilmiyoruz. gibi eşitsizliklerin çözüm kümesi bulunurken, içler dışlar çarpımı yapılamaz. Çünkü paydadaki f(x), h(x) ve m(x) in pozitif ya da negatif olduğunu bilmiyoruz. |
Uyarı
 gibi eşitsizliklerin çözüm kümesi bulunurken, g(x) = 0 ın kökleri kesri tanımsız yapacağından çözüm kümesine dahil edilmez. gibi eşitsizliklerin çözüm kümesi bulunurken, g(x) = 0 ın kökleri kesri tanımsız yapacağından çözüm kümesine dahil edilmez. |
C. İKİNCİ DERECEDEN DENKLEMLERİN KÖKLERİNİN İŞARETLERİNİN İNCELENMESİ
ax2 + bx +c = 0 denkleminin köklerinin varlığını D, köklerinin işaretini  belirler.
belirler.
a × c < 0 ise denklemin farklı iki reel kökü vardır.
a × c > 0 ise denklemin denklemin köklerinin varlığı ile ilgili kesin bir şey söylenemez.
ax2 + bx + c = 0 denkleminin kökleri x1 ve x2 olsun.
 olmalıdır.
olmalıdır. olmalıdır
olmalıdır
Bir veya daha fazla değişken içeren birbirine eşit iki niceliğin matematiksel ifadesine denklemdenir. Denklemlerin ifade edilmesinde “=” sembolü kullanılır.
Örneğin;
2x+4 = 7, 4x+1 = 2x-3, x2-1 ,= 5 ifadeleri birer denklemdir.
2x+4 = 7, 4x+1 = 2x-3, x2-1 ,= 5 ifadeleri birer denklemdir.
a, b ∈ R ve a ≠ 0 olmak üzere, ax+b=0 şeklinde ifade edilen denklemlere birinci dereceden bir bilinmeyenli denklemler denir. Burada “x” değişken olarak adlandırılır.
Örnek:
2x + 1 = 8 ifadesi, değişkeni “x” olan birinci dereceden bir denklemdir.
3n + 1 = n – 2 ifadesi, değişkeni “n” olan birinci dereceden bir denklemdir.
2x + 1 = 8 ifadesi, değişkeni “x” olan birinci dereceden bir denklemdir.
3n + 1 = n – 2 ifadesi, değişkeni “n” olan birinci dereceden bir denklemdir.
Bir niceliğin diğer bir nicelikten büyük veya küçük olma durumunu belirten ifadelere eşitsizlik denir. Eşitsizliklerin ifade edilmesinde “<, ≤, >, ≥ ” sembolleri kullanılır.
a, b ∈ R ve a ≠ 0 olmak üzere ,ax+ b > 0, ax+b < 0, ax + b ≤ 0, ax + b ≥ 0 şeklinde ifade edilebilen eşitsizliklere birinci dereceden bir bilinmeyenli eşitsizlikler denir.
Bir denklemi veya eşitsizliği sağlayan sayıların kümesine o denklemin veya eşitsizliğin çözüm kümesi denir.

























































































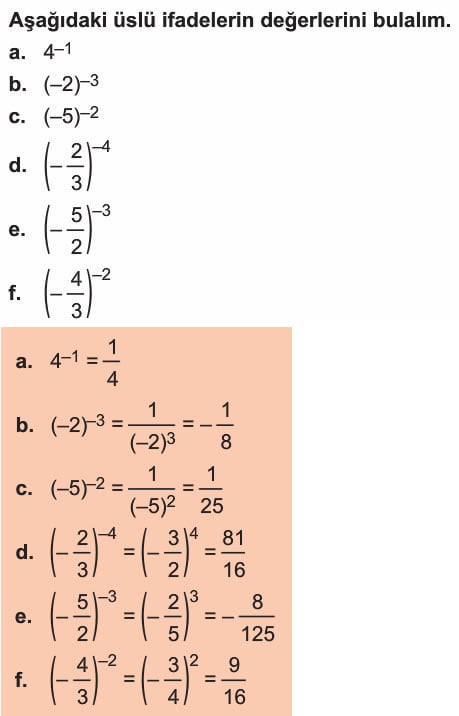




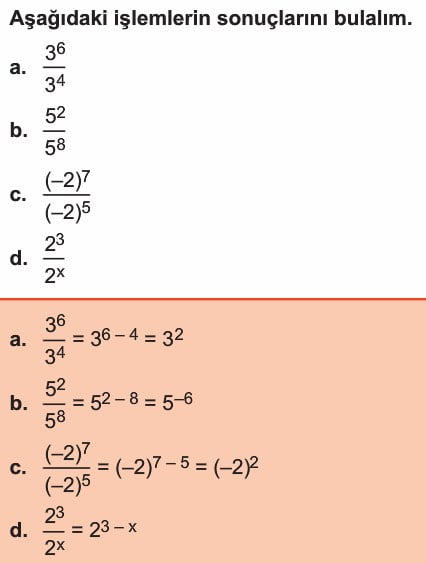
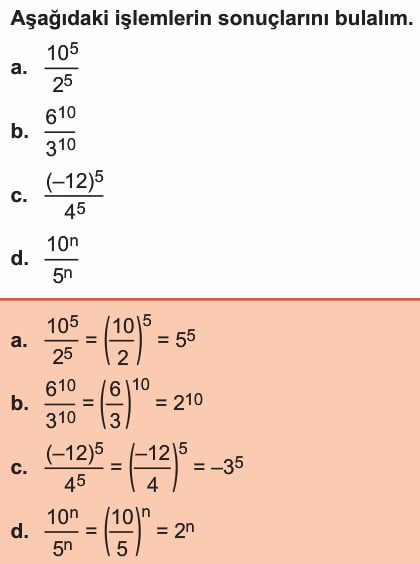
















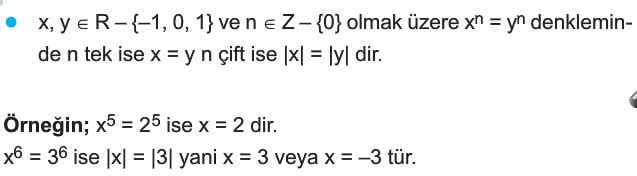











7 ile bölünebilme kuralları - 7 ile bölünebilme kuralları
YanıtlaSil3 ile bölünebilme: Sayının rakamları toplamı 3 veya 3 'ün katı ise sayı 3 'e tam bölünür.
4 ile bölünebilme: sayının son iki rakamı 00 ise veya 4 ile tam bölünebiliyorsa sayı 4 'e tam bölünür.
Bir örnek yapalım. Sayımız 10634232 olsun. ( 10, 63, 42, 32 ) Kendisinden bir küçük bir büyük 7 'nin katı sayıları çıkaralım.
YanıtlaSil